Une qu’on appellera “dessinée” et une qu’on appellera “abstraite”
La difficulté du travail géométrique avec des élèves de collège-lycée n’est pas nouvelle, notamment à cause des malentendus fréquents entre élèves et enseignant·es sur cette question. Ce texte pointe une source de malentendus : l’existence simultanée et imbriquée de “deux géométries” dans la géométrie plane et des pistes de travail pour résoudre ces malentendus. Ce texte est le fruit d’échanges d’un professeur de mathématiques de collège et de lycée, contributeur de programmes 2016, engagé avec des collègues dans la rédaction de guides pour l’enseignant·e et d’une enseignante chercheure en didactique des mathématiques travaillant sur la géométrie.
Alors que le document ressource de 2016 sur la géométrie plane en cycle 4 préconise de distinguer explicitement ces deux géométries avec les élèves, peu d’enseignant·es de mathématiques le font encore. Pourtant, en plus de réduire l’échec et de donner du sens, cette explicitation est doublement émancipatrice pour les élèves : d’une part, cela leur permet de comprendre la nécessité de produire des textes pour démontrer des résultats géométriques, d’autre part ils/elles développent un regard réflexif sur leur pratique géométrique (quelle est la nature des figures que j’étudie ?).
Au passage, notons qu’un malentendu similaire existe avec les fonctions, problème encore plus méconnu (voir le livre Des maths ensemble et pour chacun seconde, CANOPÉ, 2019).
Pourquoi distinguer explicitement deux géométries planes ?
Exemple 1.
Quand on lui demande la longueur de la diagonale d’un carré de côté 1 dm, Camélia, élève de CM2, dessine un carré sur son cahier, mesure sa diagonale et répond 14,2 cm ou quelque chose d’approchant. Le/la professeur·e valide sa réponse.
On pose la même question à Tom, élève de quatrième. Il utilise la même méthode que Camélia, répond 14,1 cm, mais cette fois-ci, le/la professeur·e n’accepte pas sa réponse.
Pourquoi une telle différence ? Pourquoi mesurer sur le dessin ne suffit-il plus en quatrième et pourquoi faut-il raisonner autrement? Parce que prendre des mesures avec un instrument entraîne une certaine imprécision ? Cela invaliderait l’utilisation de tout instrument de mesure dans la vie usuelle, les corps de métier du bâtiment…
Non, il y a une autre raison, qui peut être source de nombreux malentendus. Le contrat lié au travail géométrique a changé : le/la professeur·e de quatrième attend une réponse “théorique” de mathématicien·ne. Tom ne comprend pas pourquoi il ne peut plus se contenter de mesurer pour trouver la longueur d’un segment qu’il a dessiné sur son cahier.
Exemple 2
Considérons l’exercice suivant :
ABC est un triangle rectangle en B tel que AB = 4 cm et BC = 6 cm.
(d) est la droite parallèle à [BC] passant par A. (e) est la droite parallèle à [AB] passant par C.
D est le point d’intersection de (d) et (e).
I est le milieu de [AC].
Les points B, I et D sont-ils alignés ?
Alif, élève de cinquième, dessine soigneusement le triangle et les deux droites, place les points D et I, et finalement constate à l’aide de sa règle que les points sont alignés. À la demande du professeur, Alif pose ensuite son dessin sous la caméra (le dessin est alors projeté à toute la classe) et montre à l’aide de sa règle que B, I et D sont alignés. Beaucoup d’élèves semblent convaincus par l’argument d’Alif et là, coup de théâtre : le/la professeur·e dit que ce n’est pas bon parce que vérifier à la règle n’est pas assez précis ! Il zoome sur le dessin et constate qu’effectivement, il y a un très léger décalage entre I et la règle placée le long de la droite (BD). Il poursuit en disant qu’il faut faire une démonstration. Beaucoup d’élèves, Alif en tête, sont alors très perplexes ! Certain·es font confiance à leur professeur·e et se lancent dans la démonstration…
Plutôt que de pointer l’imprécision du dessin – une telle imprécision existera toujours – l’enseignant·e devrait dire : “Ta réponse aurait été satisfaisante à l’école, mais maintenant tu es au collège. La question que je posais concernait un rectangle et des points théoriques, pas le rectangle et les points qui sont sur ton cahier de brouillon…”.
C’est la nature des objets étudiés, abstraits-théoriques ou dessinés-matériels, qui caractérise chacune des deux géométries et qui détermine la validité des arguments.
Pour bien différencier ces deux cas :
– quand le but de l’exercice est de faire un dessin ou de répondre à une question concernant un dessin, nous disons aux élèves que nous faisons de la géométrie dessinée ;
– quand la question posée concerne un objet abstrait, nous disons aux élèves que nous faisons de la géométrie abstraite.
Si ces deux géométries se distinguent clairement par la nature des objets étudiés, elles ne s’excluent pour autant pas l’une l’autre, au contraire elles se complètent :
– la construction d’une figure complexe (question de géométrie dessinée) peut donner lieu à des raisonnements sur des figures abstraites (incursion en géométrie abstraite) avant de revenir au dessin ;
– pour résoudre une question concernant un objet abstrait, un élève peut commencer par faire une figure qui lui permettra de faire une conjecture (géométrie dessinée) puis effectuer des déductions (phrases ou calculs) à partir de ce qui est connu, seuls arguments acceptables en géométrie abstraite.
Éviter les amalgames
L’amalgame entre les deux géométries est source de confusion pour les élèves. Il est pourtant fréquent dans les manuels et on le trouve aussi par exemple dans l’énoncé du premier exercice du DNB 2014.
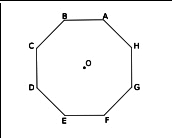
Voici un octogone régulier ABCDEFGH.
1. Représenter un agrandissement de cet octogone en l’inscrivant dans un cercle de rayon 3 cm. Aucune justification n’est attendue pour cette construction.
2. Démontrer que le triangle DAH est rectangle.
3. Calculer la mesure de l’angle .
Analysons cet exercice. La question 1. se situe dans le cadre de la géométrie dessinée, le dessin étant sans doute validé par un calque fait par le correcteur. La construction de l’octogone dans le cercle demande d’abord une analyse de la figure (travail en géométrie dessinée) et/ou la connaissance des propriétés d’un polygone régulier. L’analyse du dessin passe par le tracé de certains diamètres et la détermination d’angles (avec rapporteur ou par déduction de la régularité de l’octogone). La construction proprement dite dépend des instruments disponibles. On voit au passage que des raisonnements sont nécessaires en géométrie dessinée.
Les questions 2. et 3. emploient les termes “Démontrer” et “Calculer”. Cela sous-entend, pour l’élève initié, qu’elles sont posées en géométrie abstraite : il n’est pas licite de prendre des mesures sur le dessin pour annoncer la réponse.
D’une question à l’autre, l’élève doit changer de point de vue sur le dessin et de façon d’argumenter : il y a de quoi le perturber ! Une difficulté de cet exercice est le risque d’amalgame entre les deux géométries. D’où l’intérêt de les distinguer explicitement en classe.
La géométrie dessinée
L’élève entre dans la géométrie plane en général par le point de vue géométrie dessinée : au cycle 3 (1), il sait reconnaître des figures ou des relations entre figures ou points (comme l’alignement, la cocyclicité, la perpendicularité, le parallélisme, la comparaison de longueurs, d’angles, d’aires) globalement, mais aussi par des actions qu’il peut mener sur ces figures : les superposer, les découper, les plier, contrôler des propriétés aux instruments, utiliser des déductions qu’il peut construire à partir de la figure. Ces actions sont licites dans la géométrie dessinée : elles permettent d’obtenir de nouveaux résultats qui sont au moins valables sur les figures étudiées.
La géométrie dessinée étudie des objets plutôt matériels (traces graphiques sur le papier ou traces virtuelles sur l’écran d’ordinateur), mais ce sont déjà pour certains des objets mentaux : un trait droit sur le papier, s’il est nommé droite, doit être pensé comme rectiligne droit illimité, infini.
Le raisonnement n’est pas absent de la géométrie dessinée, ni la connaissance des propriétés des figures, déjà nécessaire pour des vérifications instrumentales. Voici le travail d’un élève de sixième à qui on demandait de tracer à main levée des symétriques par rapport à une droite.
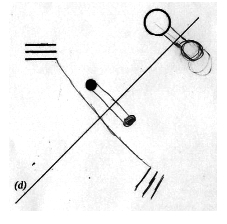
Les traits de construction qu’il a dessinés laissent supposer qu’il a compris que (A) un segment joignant un point et son symétrique est perpendiculaire à l’axe et (B) son milieu est sur l’axe. Même s’il n’a pas encore à proprement parler étudié un objet théorique en tant que tel, cet élève a déjà parcouru une partie du chemin qui le conduira vers la géométrie abstraite. Par contre la superposabilité des figures symétriques (égalité des angles et longueurs) n’est pas intégrée au dessin (mais peut-être connue de l’élève).
On pourra poursuivre ce chemin en nommant et explicitant les propriétés (A) et (B), tout en gardant à l’esprit que le fait que ces deux propriétés sont caractéristiques de la relation entre un point et son symétrique par rapport à un axe, est une connaissance de géométrie abstraite.
La géométrie abstraite
La géométrie abstraite étudie des objets théoriques, abstraits, qu’on peut représenter par des schémas par nature imparfaits, appelés figures (2). Ces objets sont définis par un texte, éventuellement accompagné par une figure codée, par exemple : “ABCD est un carré de côté (3) 3 cm et de centre O”. On ne peut obtenir des résultats nouveaux sur ces objets qu’à l’aide d’un raisonnement s’appuyant sur des propriétés établies au préalable. On peut représenter le carré ABCD par une figure, mais pour autant, l’existence d’un carré théorique n’est pas facile à concevoir pour tous les élèves.
En géométrie abstraite, les dessins sont donc toujours là, mais le regard porté sur eux a changé : le texte prime sur le dessin. Il ne faut voir sur le dessin que ce qui est déclaré vrai par un texte associé ou des signes conventionnels (les codages) qui rendent compte de relations géométriques : par exemple un carré à l’intersection de deux droites signifie que les droites sont perpendiculaires, deux signes identiques sur deux segments signifient que les segments ont la même longueur,…
En géométrie abstraite, le dessin seul ne suffit plus pour obtenir les informations, il est nécessaire de croiser le regard sur le dessin avec ce que dit le texte : c’est très nouveau pour les élèves et assez déboussolant. En contrepartie le fait de se dégager d’un dessin particulier étend la portée des résultats à toutes les figures définies par le même texte !
Faut-il pour autant ne plus du tout s’appuyer sur le dessin ? Non, crieront les géomètres. Non, car un dessin concentre en une seule image beaucoup d’informations et peut aider à faire une conjecture. Le raisonnement peut aussi s’appuyer sur le dessin car sur celui-ci, il est plus facile de repérer (mais cette facilité n’est pas innée) des figures qui peuvent faire penser à des définitions, des propriétés, des théorèmes : il faut alors vérifier sur le texte que les conditions d’application d’une définition, d’une propriété, d’un théorème sont remplies. Ce qui permet souvent d’obtenir un nouveau résultat.
Le dessin est un auxiliaire irremplaçable, mais il ne peut exister seul, ni être “lu” sans le texte qui l‘accompagne ou les codages ajoutés sur le dessin pour rendre compte des propriétés données.
Comment introduire l’idée de géométrie abstraite au cycle 4 ?
Nous proposons une manière de faire mais il y en a bien sûr beaucoup d’autres. Cette approche est pensée pour faire prendre conscience aux élèves de la nécessité d’une géométrie abstraite pour l’activité géométrique.
Étape 1
La situation ci-dessous a été créée par Guy Brousseau (4), chercheur français en didactique des mathématiques, qui a été récompensé par le premier prix Félix Klein (2003) par le Comité International d’Éducation Mathématique, pour l’œuvre de toute une vie. Nous nous appuyons sur elle pour motiver l’entrée des élèves en géométrie abstraite et montrer le rôle que doit jouer l’enseignant·e dans ce “passage”. Cette situation est également intéressante au cycle 4 comme situation de reprise de la notion de médiatrice (il est nécessaire que soient déjà connues des élèves les deux définitions/ propriétés de la médiatrice vues en fin de cycle 3 : droite perpendiculaire à un segment en son milieu et lieu des points à égale distance des extrémités du segment).
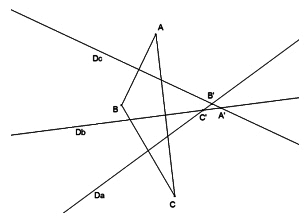
L’enseignant·e demande à ses élèves de tracer les trois médiatrices d’un triangle ABC très aplati et de nommer les points d’intersection des médiatrices. Il a lui-même préparé un “très grand” triangle ABC (dont un angle est “très obtus”) sur une feuille A3 ; il a tracé des droites (très proches des médiatrices de chaque côté) qui se coupent deux à deux à l’extérieur en un petit triangle A’B’C’, appelé le cotriangle de ABC.
Il/elle avoue être insatisfait de la taille du petit triangle qu’il a fait et demande aux élèves de trouver un triangle ABC dont le co-triangle A’B’C’ est le plus grand possible. Les élèves s’acharnent sans réussir à agrandir le co-triangle. Il se peut qu’ils déclarent que ce n’est pas possible, certains pouvant même déclarer que les trois médiatrices se coupent. Finalement les élèves émettent l’hypothèse que ce n’est pas possible : au contraire le co-triangle est souvent plus petit, les trois points A’, B’, C’ semblent n’en former qu’un seul. L’enseignant peut alors questionner que ce qui se passerait pour une figure très grande par exemple qu’on tracerait dans la cour de récréation.
L ’idée de cette situation est de générer une incertitude, voire un conflit, entre réponses différentes. L’enseignant·e déclare alors qu’il existe une façon de trancher : on ne s’intéresse plus aux figures dessinées mais à la “figure abstraite”, définie par ses propriétés. On passe ainsi en “géométrie abstraite”. L’enseignant·e rédige alors un petit texte au tableau qui sera recopié ou collé sur le cahier à la suite des essais de construction collés.
A’ est sur la droite (Db) et (Db) est médiatrice du segment [AB] : donc A’A=A’B
A’ est sur la droite (Dc) et (Dc) est médiatrice du segment [BC] : donc A’B=A’C
On peut donc dire que A’A=A’C : cela prouve que A’ est aussi sur la médiatrice du segment [AC], la droite (Da).
A’ est sur la droite (Db), sur la droite (Dc) et sur la droite (Da) : donc les trois droites se coupent en UN SEUL point.
En géométrie abstraite, le petit triangle A’B’C’ n’existe pas.
En géométrie abstraite, les trois médiatrices d’un triangle se coupent en un seul point.
Cela est vrai pour tout triangle (aussi grand soit-il).
L’enseignant·e conclut en demandant aux élèves ce qu’ils pensent maintenant des dessins où apparaissait un co-triangle. L’enseignant·e avoue avoir triché pour obtenir un si grand co-triangle. Son objectif est que les élèves apprennent que des dessins sont toujours des illustrations imparfaites des objets théoriques, abstraits, même si on essaie d’être très précis. On a démontré (c’est-à-dire prouvé en géométrie abstraite) les trois médiatrices d’un triangle, quel qu’il soit, sont concourantes car le raisonnement écrit est indépendant de la taille, de la forme du triangle. Cela explique aussi pourquoi il est impossible de dessiner un triangle avec un grand co-triangle.
Étape 2
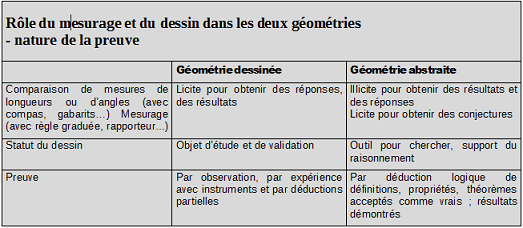
Dans la foulée, l’enseignant·e fait travailler les élèves sur la différence entre les deux géométries. Il installe géométrie dessinée et géométrie abstraite dans la classe, explicite les différences entre les deux, notamment la nature des objets étudiés (matériel versus théorique/ abstrait), les actions “licites” (ou pas) en géométrie dessinée et en géométrie abstraite (voir un tableau pour l’enseignant·e en annexe de cet article), le fait que des définitions “minimales” ne sont nécessaires qu’en géométrie abstraite, et qu’en géométrie dessinée, on cite toutes les propriétés d’une figure.
Étape 3
Il est intéressant de proposer, à la suite, des exercices posés en géométrie abstraite pour permettre aux élèves de commencer à se familiariser avec cette géométrie. On trouvera des exemples d’exercices dans la partie suivante : “Exemples d’exercices de géométrie abstraite”.
Étape 4
Un peu plus tard dans l’année, sans crier gare, l’enseignant·e pourra proposer des situations de géométrie dessinée qui, telle la situation de l’étape 1, seront éclairées une fois considérée la situation correspondante en géométrie abstraite.
Exemple 1
L’enseignant·e demande aux élèves, en classe au moins pour C et E, de construire sur feuilles blanches, à la règle et au compas, des triangles dont il donne les longueurs en centimètres : triangle A (5, 10, 7) ; triangle B (12, 6, 8) ; triangle C (6, 11, 5) ; triangle D (6, 8, 10) ; triangle E (5, 4, 12).
C’est d’abord une façon de revoir ensemble la construction d’un triangle à la règle et au compas. Il n’y aura pas de correction collective au tableau (sauf par l’usage d’un logiciel de géométrie dynamique qui montre le film d’une construction au moins) ; l’appréciation de la réussite individuelle se fera par comparaison avec le transparent de l’enseignant·e. L’enseignant·e s’arrête en particulier sur le triangle C pour lequel les réponses seront variées : (I) production d’un triangle effectif assez aplati, (II) réponse que ce n’est pas possible de faire un triangle avec ces longueurs, (III) réponse de “normand” : impossible si on commence par le côté 11, et triangle très aplati si on commence par le côté 6 ou le côté 5. L’enseignant·e suscite le débat pour écouter les arguments et mieux connaître le point de vue de ses élèves. Si aucun·e élève ne suggère de passer en géométrie abstraite, il/elle tranche le débat : le travail de construction s’est fait en géométrie dessinée, qui peut donner lieu à des productions différentes, même si très proches. En géométrie abstraite, le triangle C n’existe pas (ou il est réduit à un segment) : on peut le prévoir car une des longueurs est la somme des deux autres (11=6+5). Il existe un théorème en géométrie abstraite qui valide cela : le plus court chemin entre deux points est la ligne droite. Ainsi une ligne brisée de deux segments reliant les deux extrémités du segment le plus long sera toujours plus longue que ce segment.
Exemple 2
L’enseignant·e demande à chaque élève de tracer sur une feuille unie un (grand) quadrilatère convexe : a priori dans la classe seront obtenus des quadrilatères de formes et tailles différentes. Si ensuite chaque élève trace le quadrilatère des milieux (à définir par l’enseignant·e), chacun·e ou presque pourra constater à l’œil et vérifier aux instruments que chaque quadrilatère des milieux est un parallélogramme, voire un losange ou un rectangle. Grâce à un logiciel de géométrie dynamique, ce constat peut être étendu à un très grand nombre de cas : le quadrilatère des milieux est toujours “au moins” un parallélogramme. L’enseignant·e pose alors la question : est-ce “vraiment” vrai pour tous les quadrilatères des milieux, quelle que soit la forme, la taille, du quadrilatère de départ ? Est ce vrai, pour un quadrilatère de départ qui aurait comme dimensions des “dizaines de kilomètres”, tellement grand qu’on ne le verrait pas en une seule fois ? Les élèves suggèrent alors de le regarder d’un avion, mais quels instruments utiliser alors pour vérifier les propriétés du quadrilatère des milieux ?
Ici encore, quelqu’un·e, un·e élève ou le professeur·e, propose de changer de point de vue et de s’intéresser à l’objet théorique défini par un texte, c’est-à-dire de passer en géométrie abstraite. Dans le cadre de la géométrie abstraite, on peut affirmer, grâce à un raisonnement qui s’appuie sur le théorème de Thalès ou sur le théorème des milieux, que le quadrilatère des milieux est un parallélogramme. Cette certitude théorique permet de dire, sans être obligé de vérifier, que tous les quadrilatères des milieux, même les très grands, sont aussi des parallélogrammes. Travailler sur des objets théoriques permet de résoudre le problème pour l’infinité des quadrilatères des milieux dessinés. Ce qui montre aux élèves l’intérêt de la géométrie abstraite relativement à la géométrie dessinée.
Exemples d’exercices en géométrie abstraite
Avant de proposer un exercice de géométrie abstraite, il est nécessaire de s’assurer que les élèves connaissent une “axiomatique locale”, c’est-à-dire un ensemble de quelques définitions et propriétés qui pourront être convoquées par les élèves lors du raisonnement déductif qu’ils devront faire pour répondre à la question.
Exemple 1
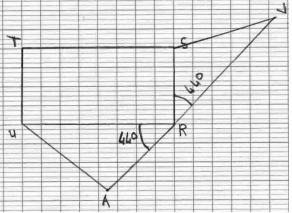
L’énoncé suivant, qui comporte une figure, est distribué aux élèves.
RSTU est un rectangle.
RSV et RUA sont des triangles extérieurs au rectangle tels que les angles SRV et URA mesurent 44° chacun
Voici une figure ci-contre. Les points A, R et V sont-ils alignés ?
Après une phase de travail individuel, les élèves mettent en commun par groupes de trois ou quatre. L’enseignant·e aura pris soin de constituer des groupes hétérogènes, chaque groupe comportant un élève susceptible d’avoir assimilé une grande partie de ce qui a été fait dans l’étape 2 de la partie précédente. Au sein de chaque groupe, le débat devrait alors être riche, certain·es constatant l’alignement sur la figure, d’autres n’étant pas d’accord car ils ont compris que la question ne concerne pas les points A, R et V du dessin.
Le raisonnement que les élèves vont mettre en place s’appuie sur une axiomatique très légère : la définition d’un rectangle en géométrie abstraite et la formule donnant la mesure d’un angle “composé” (vue en géométrie dessinée et qui reste valable en géométrie abstraite).
Exemple 2
RPS est un triangle abstrait tel que l’angle PRS mesure 50°.
Le point Q est symétrique du point P par rapport à la droite (RS).
Quelle est la nature du triangle PQR ? Justifie ta réponse.
Remarque : la présence dans la consigne de l’expression “Justifie ta réponse” est parfois vue par l’enseignant·e comme indicateur d’une demande en géométrie abstraite. Ce n’est pas clair pour les élèves, qui à juste titre, ont l’impression de justifier quand ils vérifient leurs hypothèses en prenant des informations sur le dessin avec des instruments. En réalité le seul terme qui relève de géométrie abstraite est démontrer.
Il est intéressant de prévoir un temps de recherche en groupe et de laisser les groupes résoudre l’exercice à leur façon pour comparer ensuite en plénière les types de réponses. C’est l’occasion de préciser à nouveau les deux géométries.
Le groupe A fait un dessin de l’angle R (en respectant ou pas sa mesure) ; il place un point P et trace la perpendiculaire à (RS) passant pas P, puis reporte la distance entre P et (RS) pour placer le point Q : il déclare RPQ est un triangle isocèle car RQ =RP.
Le groupe B fait le même dessin, compare les longueurs RP et RQ et voit qu’elles sont égales. Puis il déclare : (PQ) est perpendiculaire à (RS), et (RS) passe par le milieu du segment [PQ](5). (RS) est donc la médiatrice de [PQ]. RP=RQ (6). Le triangle PQR est isocèle en R.
Tout d’abord les deux réponses précédentes montrent des raisonnements. Le groupe A a justifié sa réponse (le fait que le triangle est isocèle) ; par contre il ne précise pas comment il a obtenu cette information ; sa justification est incomplète. S’il ajoute “j’ai mesuré les longueurs (ou je le vois sur mon dessin)”, il a justifié en géométrie dessinée. Il n’a pas respecté la consigne initiale.
Le groupe B travaille d’abord en géométrie dessinée. Il passe ensuite à un enchaînement d’arguments qui montre qu’il cherche à répondre en géométrie abstraite, ce qu’il réussit fort bien.
Modéliser un problème de géométrie plane
Considérons cet exercice.
Voici un homme et deux poteaux. Trouver la hauteur h du second poteau en s’appuyant sur le schéma ci-dessous.
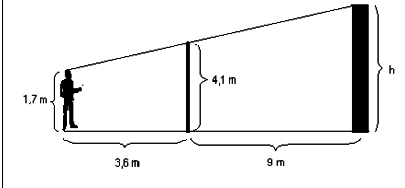
Ce problème au départ n’est pas un problème posé en géométrie abstraite dans la mesure où un grand nombre d’informations ne sont disponibles que sur le dessin : on peut supposer que les poteaux sont perpendiculaires au sol, on pourrait dire que donc que homme et poteaux sont parallèles. Il y a plusieurs façons de répondre à cette question.
Traitement en géométrie dessinée :
On fait un dessin précis à l’échelle 1/100 (ou plus adapté 1/50), ce qui nécessite déjà des connaissances géométriques. Un mesurage de h sur le dessin avec une règle graduée fournira une mesure approximative de la hauteur du poteau, par exemple entre 9,9 et 10,3 m.
Traitement en géométrie abstraite :
Moyennant l’intégration d’hypothèses “raisonnables” – deux droites coupées par trois droites parallèles, les “verticales” – il s’agit de déduire la longueur cherchée uniquement de données connues ou sûres. Les parallèles peuvent évoquer le théorème de Thalès. Si l’élève connaît ce théorème et est apte à décomposer/recomposer une figure, il peut penser à insérer dans la figure une sous-figure triangulaire, dont les longueurs puissent se déduire des longueurs données et qui permette de trouver la longueur (ou une partie de longueur manquante) par une déduction licite en géométrie abstraite, ce qui donne h = 10,1 m.
Peut-on parler, dans l’absolu, d’une meilleure solution ? Dans ce contexte d’évocation de la réalité, un traitement en géométrie dessinée est très efficace, d’autant plus que les nombres proposés au départ peuvent apparaître comme des résultats de mesurage, donc prétexte à une certaine imprécision. On peut faire valoir que la résolution en géométrie abstraite présente une économie de tracé (un dessin à main levée suffit) et offre une généralisation plus rapide : c’est vrai (et ce pourrait être un argument pour l’entrée dans la géométrie abstraite) mais pour un problème local, les deux démarches offrent globalement le même coût (dessin versus Thalès) et nécessitent des raisonnements non triviaux mettant en jeu de la proportionnalité.
Conclusion
Les élèves sont souvent pris dans des tâches qui relèvent implicitement de géométries différentes (géométrie dessinée et géométrie abstraite). Nommer et repérer ces deux géométries devraient permettre aux enseignant·es d’analyser la tâche en termes de géométrie sollicitée, de qualifier des réponses d’élèves, de hiérarchiser les exercices. Expliciter aux élèves, à l’occasion d’exercices, les deux géométries, leurs spécificités, les raisons pour lesquelles elles sont toutes les deux nécessaires, devrait permettre à ceux et celles-ci de mieux comprendre les attentes de l’enseignant·e.
Jean-Philippe Rouquès, professeur de mathématiques dans le secondaire à Nantes
mars 2016
(1) Dans les programmes 2016 de cycle 3, les activités de géométrie dessinée (reproduction et construction de figures sous contrainte d’instruments) occupent une place importante.
(2) Un des sens de figurer est représenter.
(3) On pourrait considérer qu’une unité concrète telle que le centimètre n’a pas sa place en géométrie abstraite. Cependant, par commodité pédagogique, nous ne nous interdisons pas l’emploi de telles mesures concrètes en géométrie abstraite.
(4) Brousseau G., Les propriétés didactiques de la géométrie élémentaire. Séminaire de Didactique des Mathématiques, Crète, Rethymon,2000. En ligne https://hal.archives-ouvertes.fr/hal-00515110/fr/
(5) L’enseignant·e peut faire ajouter ici : car Q et P sont symétriques par symétrie axiale.
(6) L’enseignant·e peut faire ajouter ici : car R est sur (d) médiatrice de [PQ].
Pour aller plus loin :
■ Catherine Houdement et Alain Kuzniak, Géométrie et paradigmes géométriques, Petit x n°51, 1999. En ligne ici
■ Quand deux droites sont à peu près égales ou le versant géométrique du presque égal, Petit x n°61, 2003. En ligne ici
■ Paradigmes géométriques et enseignement de la géométrie, Annales de Didactique et de Sciences Cognitives n° 11, 2006. En ligne ici
■ Une analyse et des propositions d’enseignement des codages sur les figures, Groupe Didactique IREM de Montpellier.
■ Le codage, quand, comment, pourquoi ?, IREM de Montpellier, juin 1998.
Laisser un commentaire
Vous devez vous connecter pour publier un commentaire.